Простая реализация пролога о многоагентной аргументации

Question

Новое для логического программирования (Prolog). Переходите на простой вопрос, но не знаете, как закодировать его в прологе.

Вопрос такой, как у вас есть несколько аргументов: аргумент (a), аргумент (b) ... и несколько атак, таких как атака (a, b), что означает аргумент аргумента атак b. Поэтому, учитывая аргумент, я хочу узнать, является ли он обоснованным. «Заземленный» для аргумента означает, что если b атакует a, тогда существует другой аргумент, скажем c атак b. Если ни один аргумент не атакует c, мы говорим, что a и c заземлены.

Можете ли вы привести пример того, как реализовать эту заземленную/1 программу для достижения этой цели.

Не уверен, что я проясню .... Но добро пожаловать, чтобы дать какой-либо совет (или код) !!

Answer 1

Что я понял из вашего объяснения, аргумент обоснован, если нет других обоснованных аргументов, атакующих его.

Вы можете определить процедуру grounded/1 которая подчиняется это правило простого в прологе:

grounded(A):- 
    argument(A), % A is an argument 
    \+    % for which there does not exist 
    (
    attack(B, A), % an attacker 
    grounded(B) % which is grounded 
). 

[Редактировать после замечания OP]: Если вам приходится иметь дело с циклами, то вам, вероятно, нужно держать список посещаемых «атак», без каких-либо запрещающих циклов:

grounded(A):- 
    grounded(A, []). 


grounded(A, L):- 
    argument(A), 
    \+ 
    (
    attack(B, A), 
    \+ member(B, L), % Here we forbid cycles 
    grounded(B, [A|L]) % We add the current argument to the list of forbidden arguments 
). 

Answer 2

Я не знаю, как писать в Прологе, но заземленная семантика вычисляется исходя из аргументов, которые не были атакованы, учитывая аргумент дерева.

(Надеюсь, что это ведет @gusbro, чтобы найти правильный ответ на эту тему.)

Чтобы объяснить, как это вычислить, я познакомлю следующую функцию F (х) = {х защищает у}, где :

• 
• 
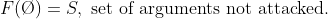
• Если один защищал аргумент атакован другим deffended аргумента, то атакуемый аргумент будет удаляться из набора.
• И так далее, пока функция не может быть более расширена с большим количеством аргументов, которые достигли минимальной фиксированной точки в F.

(Exemple 1) дал следующий график аргументации, заземленный расширение Например = {с, д, е, а}.

Итак, первая функция начинается с:

Теперь рассмотрим вычисление заземленной расширения с циклами.

(пример 2) В данной аргументации графа сильфона, е защищает б и д, но б атакован д, то она не может быть включена в заземленный семантика. С этого момента мы имеем бесконфликтный набор {e, d}. От {E, D} можно применить Агинского функцию F ({е, д}) = {е, д, а}, где д защищает от б. Применяя снова функцию F ({e, d, a}) = {e, d, a}, показывая, что {e, d, a} - минимальная фиксированная точка в F. Следовательно, {e, d, a} является заземленным расширением.

(пример 3) В дереве аргументации ниже, заземленное расширение , так как Там не аргументы, которые не были атакованы. В противном случае, если аргумент e не атаковал сам, заземленное расширение должно быть , что не так.

В этом последнем примере, цикл поднимается различными предпочтительными расширения, где вы можете использовать в качестве поддержки эквивалентного понятия маркировки аргументов, определенного в другом месте Мартина Caminada.