S-выражение для направленного ациклического графа?

Question

Как мы знаем, древовидная структура может быть представлена ​​в S-выражениях. Например

(5 (4 (11 (7()()) (2()()))()) (8 (13()()) (4() (1()())))) 

Но можно использовать S-выражение для графа (особ. DAG)? например

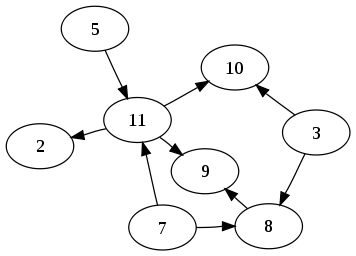
Мой второй вопрос, что является пределом топологии S-выражение может представлять?

I Googled this quesion и не мог найти подсказки, без формального фона CS, у меня возникли проблемы с этим. Пожалуйста, не закрывайте этот вопрос. Заранее спасибо!

Answer 1

Не как рекурсивная структура, как ваше двоичное дерево.

• Вы можете использовать список узлов, а для каждого магазина - узлы, к которым он имеет ребро.

  ((2()) 
      (3 (8 10)) 
      (5 (11)) 
      (7 (8 11)) 
      (8 (9)) 
      (9()) 
      (10()) 
      (11 (2 9 10))) 
  

• Вы можете сохранить список узлов и ребер.

  ((2 3 5 7 8 9 10 11) 
      ((3 8) 
      (3 10) 
      (5 11) 
      (7 8) 
      (7 11) 
      (8 9) 
      (11 2) 
      (11 9) 
      (11 10)))