В выходном слое нейронной сети, это характерно использовать SoftMax функцию для аппроксимации распределения вероятностей:Зачем использовать softmax в отличие от стандартной нормализации?
Это дорого, чтобы вычислить из показателей. Почему бы просто не выполнить преобразование Z так, чтобы все выходы были положительными, а затем нормализовались просто делением всех выходов на сумму всех выходов?
Значения q_i представляют лог-правдоподобия. Чтобы восстановить значения вероятности, вам необходимо их проинструктировать.
Одна из причин, по которой статистические алгоритмы часто используют функции потери прав на правдоподобие, состоит в том, что они более численно устойчивы: произведение вероятностей может быть представлено как очень малое число с плавающей запятой. Используя функцию потери логарифмического правдоподобия, произведение вероятностей становится суммой.
Другая причина состоит в том, что логарифмические вероятности происходят естественным образом при получении оценок для случайных величин, которые предполагается нарисовать из многомерных гауссовских распределений. См., Например, оценку максимального правдоподобия (ML) и способ ее подключения к наименьшим квадратам.
В качестве опоры, я думаю, что этот вопрос более уместен для теории СС или вычислительной науки.
q_i не подразумевает представления правдоподобия. это только когда мы используем softmax, который мы явно предполагаем. – Tom
Я нашел объяснение здесь, чтобы быть очень хорошим: CS231n: Convolutional Neural Networks for Visual Recognition.
На поверхности SoftMax алгоритм, кажется, простой нелинейный (мы распространяем данные с экспоненциальной) нормализации. Однако есть нечто большее.
В частности есть несколько различных мнений (same link as above):
Теория информации - с точки зрения теории информации, которую SoftMax функция может рассматриваться как попытка свести к минимуму перекрестное энтропию между предсказаниями и правда.
Вероятностный взгляд - с этой точки зрения мы фактически рассматриваем логарифмические вероятности, поэтому при выполнении возведения в степень мы получаем исходные вероятности. В этом случае уравнение SoftMax найти ОМП (максимальное правдоподобие оценки)
В итоге, несмотря на то, SoftMax уравнение кажется, что это может быть произвольным это не так. На самом деле это довольно принципиальный способ нормализации классификаций, чтобы минимизировать вероятность кросс-энтропии/отрицательного правдоподобия между предсказаниями и истиной.
Чтобы добавить к предыдущим комментариям, производная от функции softmax является просто softmax (1-softmax) – RZK
Я получаю причины использования кросс-энтропийной потери, но как это связано с softmax? Вы сказали: «Функция softmax может рассматриваться как попытка свести к минимуму кросс-энтропию между предсказаниями и истиной». Предположим, я бы использовал стандартную/линейную нормировку, но все равно использую Cross-Entropy Loss. Тогда я также попытаюсь свести к минимуму Cross-Entropy. Итак, как мягкий макс связан с кросс-энтропией ** кроме ** для численных преимуществ? –
Что касается вероятностного взгляда: какова мотивация поиска вероятностей журнала? Похоже, что рассуждение немного напоминает «Мы используем e^x в softmax, потому что мы интерпретируем x как log-probabilties». С теми же рассуждениями, которые мы могли бы сказать, мы используем e^e^e^x в softmax, потому что мы интерпретируем x как log-log-log-вероятности (здесь, конечно, преувеличение). Я получаю численные преимущества softmax, но какова теоретическая мотивация его использования? –
Пусть мы изменим SoftMax функцию так что выходные активаций определяются 
где c положительная постоянная. Обратите внимание, что c=1 соответствует стандартной функции softmax. Но если мы используем другое значение c, мы получаем другую функцию, которая, тем не менее, качественно похожа на softmax. В частности, покажите, что выходные активации образуют распределение вероятности, как и для обычного softmax. Предположим, что мы позволим c стать крупными, то есть c→∞. Каково предельное значение для активизации выхода a^L_j?После решения этой проблемы вам должно быть понятно, почему мы думаем о функции c=1 как «смягченной» версии максимальной функции. Это источник термина «softmax». Вы можете следить за деталями из this source (уравнение 83).
Мы рассматриваем проблему с несколькими классификациями. Прогнозируемая переменная y может принимать одно из значений k, где k > 2. По вероятности это удовлетворяет многочленному распределению, а многочленное распределение принадлежит большому семейству, называемому экспоненциальным семейством. Согласно свойству экспоненциальных распределений семейств, мы можем восстановить вероятность P(k=?|x), это совпадает с формулой softmax.
За дополнительной информацией и официальным подтверждением ссылки CS229 lecture notes (Softmax Regression).
Полезный трюк обычно выполняется для softmax: softmax (x) = softmax (x + c), то есть softmax инвариантен к постоянным смещениям на входе.
Существует один хороший атрибут SoftMax по сравнению со стандартной нормализации.
Он реагирует на низкую стимуляцию (думает, размытое изображение) ваша нейронной сети с достаточно равномерным распределением и высокой стимуляцией (то есть. Большое количество, думает, четкое изображение) с вероятностями, близким к 0 и 1.
В то время как стандарт нормализация не волнует, пока пропорция одна и та же.
Посмотрите, что происходит, когда мягкий максимум имеет в 10 раз больший вклад, т.е. вашей нейронная сеть получила четкое изображение и много нейронов активировались
>>> softmax([1,2]) # blurry image of a ferret
[0.26894142, 0.73105858]) # it is a cat perhaps !?
>>> softmax([10,20]) # crisp image of a cat
[0.0000453978687, 0.999954602]) # it is definitely a CAT !
А затем сравнить его со стандартной нормализацией
>>> std_norm([1,2]) # blurry image of a ferret
[0.3333333333333333, 0.6666666666666666] # it is a cat perhaps !?
>>> std_norm([10,20]) # crisp image of a cat
[0.3333333333333333, 0.6666666666666666] # it is a cat perhaps !?
Этот ответ лучше всего иллюстрирует * воздействие * использования возведения в степень, а не фокусирование на теоретических основах. (что здорово). Он должен быть включен в начало верхнего ответа. Посмотрев, как и в какой степени степень возвышения распространяется на значения, главный ответ помогает объяснить, почему вы этого хотите. –
выбора SoftMax функции кажется как-то произвольно, поскольку есть много других возможных функций нормализующих. Таким образом, неясно, почему потеря log-softmax будет лучше, чем другие альтернативы потерь.
С «разведочными из SoftMax Альтернативы Принадлежности к сферической потере семьи» https://arxiv.org/abs/1511.05042
Авторов исследовались некоторые другие функции, среди которых Тэйлор расширение exp и так называемые сферическими SoftMax и выяснил, что иногда они могли бы работать лучше обычного softmax.
У меня был этот вопрос в течение нескольких месяцев. Похоже, мы просто ловко угадали softmax как функцию вывода, а затем интерпретировали входной сигнал softmax как логарифмические вероятности. Как вы сказали, почему бы просто не нормализовать все выходы, разделив их на сумму? Я нашел ответ в Deep Learning book Гудфеллоу, Бенгио и Курвилле (2016 год) в разделе 6.2.2.
Скажем, наш последний скрытый слой дает нам z как активацию.Затем SoftMax определяется как
ехр в SoftMax функции примерно отменяет журнал в кросс-энтропии потери, вызывая потерю быть примерно линейно по z_i. Это приводит к грубому постоянному градиенту, когда модель ошибочна, что позволяет быстро исправлять ее. Таким образом, неправильный насыщенный softmax не вызывает исчезающего градиента.
Самого популярный метод для обучения нейронной сети является максимальным правдоподобием Оценки. Мы оцениваем параметры тета таким образом, чтобы максимизировать вероятность данных обучения (размера m). Поскольку вероятность того, что весь набор данных обучения является продуктом вероятности каждого образца, легче максимизировать лог-правдоподобие набора данных и, таким образом, сумму логарифмической вероятности каждого образца, проиндексированного по k:
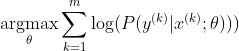
Теперь мы сосредоточимся только на SoftMax здесь с г уже дали, поэтому мы можем заменить
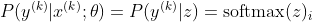
с я быть правильный класс образца -го. Теперь мы видим, что, когда мы берем логарифм SoftMax, чтобы вычислить логарифмическую вероятность сэмпла, получим:
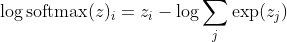
, что для больших различий в г примерно приближается к
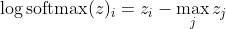
Сначала мы видим здесь линейную составляющую z_i. Во-вторых, мы можем изучить поведение max (z) для двух случаев:
Мы видим, что общее логарифмическое правдоподобие будет определяться образцами, где модель неверна. Кроме того, даже если модель действительно неверна, что приводит к насыщенному softmax, функция потерь не насыщается. Он приблизительно линейный по z_j, что означает, что мы имеем примерно постоянный градиент. Это позволяет быстро скорректировать модель. Обратите внимание, что это не относится к среднему квадрату ошибки, например.
Если SoftMax все еще кажется, что произвольный выбор для вас, вы можете посмотреть на обоснование использования сигмовидной в логистической регрессии:
Why sigmoid function instead of anything else?
SoftMax является обобщение сигмоида для многоклассовых задач оправдано аналогично.
Функция вычисляется не дорого из-за экспонентов, а потому, что вам нужно вычислить каждый qj. Экспоненциация является дешевой по сравнению с общим количеством необходимых вычислений. –