Есть ли способ конвертировать кватернион под углом?

Question

У меня есть (мировая) матрица, и она применяет перевод, поворот и масштаб в трехмерный объект. Он создается с помощью функции XMMatrixTransformation (DirectXMath), а параметр RotationQuaternion производится по вызову XMQuaternionRotationRollPitchYaw. Затем он сохраняется в файле вместе с другими данными.

Тогда мне нужно, чтобы восстановить значения, так что я могу использовать эту функцию, чтобы разложить его по каждому компоненту:

XMMatrixDecompose(&Scale, &RotationQ, &Translation, Matrix); 

Scale и перевод являются векторами и вращение кватернионов. Если матрица поворачивает объект в одной оси, я мог бы использовать это, чтобы преобразовать кватернион назад к углам:

XMQuaternionToAxisAngle(&Axis, &Angle, RotationQ); 

Он отлично работает. Но когда он вращается в двух или более осях, как я могу сделать то же самое? Есть ли способ сделать это?

PS: Мне все равно, если выходные углы не совпадают с входом. Они просто должны быть эквивалентными.

PS2: Хорошо, поэтому я последовал за ссылкой Гена (я уже там посмотрел, но не нашел то, что мне было нужно в это время). Я сделал этот код, основанный в этом уравнении я нашел в Википедии: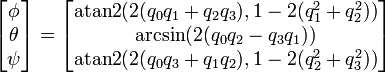

float Roll = atan2(2.0*(F.x*F.y + F.z*F.w), 1 - 2 * (F.y*F.y + F.z*F.z)); 
float Pitch = asin(2.0*(F.x*F.z - F.w*F.y)); 
float Yaw = atan2(2.0*(F.x*F.w + F.y*F.z), 1 - 2 * (F.y*F.y + F.z*F.z)); 

В выходных у меня есть разные углы. Выход кажется эквивалентным для (90°, 0°, 90°), но не для (45°, 45°, 45°).

Answer 1

У вас есть два варианта.

Вы все еще можете использовать функцию XMQuaternionToAxisAngle(), и она будет использовать ось, отличную от основных осей. Любое вращение может быть представлено как один угол, вращающийся вокруг данной оси.

С другой стороны, если вам действительно нужно получить его как углы Эйлера, нет никакой хорошей функции, чтобы сделать это за вас. Однако формулы легко доступны. Материал из Википедии:

По определению Википедии, фита угол вокруг глобальной оси Z, тета угол вокруг «нормальной оси» N (ось, которая проходит через местное происхождение и ортогонален плоскость глобальной оси Z и конечная локальная ось Z - да, это странно странно), а psi - угол вокруг локальной (то есть повернутой) оси Z.

Если бы я был лучшим математиком, я мог бы помочь вам перевести это в простое вращение X, Y, Z в глобальном пространстве, но, к сожалению, это выходит за рамки моих возможностей.

Просто знайте, что не существует строгой корреляции 1-1 между кватернионами и углами Эйлера; gimbal lock означает, что есть определенные углы, которые имеют один и тот же угол Эйлера, например. Подумайте, действительно ли вам нужны углы Эйлера - в большинстве случаев поворот по осевому углу будет работать одинаково, без значительных проблем с углами Эйлера.